Objetos Fractais em Mandelbrot

"Ao longo deste ensaio, objetos fractais naturais muito diversos, alguns dos quais, como a Terra, o céu e o oceano, nos são bastante familiares, são estudados com a ajuda de uma grande família de objetos geométricos, até agora considerados exotéricos e perfeitamente inúteis. Pretendo mostrar, pelo contrário, que estes objetos, pela sua simplicidade, diversidade e extraordinária extensão das suas novas aplicações, merecem ser rapidamente integrados na geometria elementar. Apesar do seu estudo fazer parte de campos científicos diferentes, entre os quais a geomorfologia, a astronomia e a teoria da turbulência, os objetos naturais em questão têm em comum uma forma irregular ou interrompida. Para os estudar, concebi, aperfeiçoei e utilizei extensivamente uma nova geometria da natureza.

A noção que lhe serve de fio condutor será designada por um de dois neologismos equivalentes, 'objeto fractal' ou 'fractal', termos que formei, pela necessidade que me surgiu com este livro, a partir do adjetivo latino fractus, que significa 'irregular' ou 'quebrado'.

Será necessário definir uma figura fractal de modo rigoroso, para em seguida dizer que um objeto real é fractal por se assemelhar à figura geométrica que constitui o modelo? Considerando que um tal formalismo seria prematuro, adotei um método muito diferente: um método baseado numa caracterização aberta e intuitiva, onde os avanços se efetuam por retoques sucessivos.

O subtítulo sublinha que o meu objetivo inicial consiste em descrever, a partir do exterior, a forma de diversos objetos. Logo que esta primeira fase seja bem sucedida, a prioridade transita de imediato da descrição para a explicação: da geometria para a dinâmica, a física e por aí adiante.

O subtítulo indica ainda que, para conseguir a irregularidade fractal, coloco em discussão as construções em que predomina o acaso.

Por fim, o subtítulo explicita que uma das características principais de todo objeto fractal é a sua dimensão fractal, que será representada por D. Esta é uma medida do grau de irregularidade e de fragmentação. Um fato muito importante: ao contrário dos números dimensionais correntes, a dimensão fractal pode muito bem ser uma fração simples, como 1/2 ou 5/3, ou mesmo um número irracional, como log 4/log 3 = 1,2618... Assim, é conveniente dizer, a respeito de certas curvas planas muito irregulares, que a sua dimensão fractal se situa entre 1 e 2, a respeito de certas superfícies muito enrugadas e cheias de pregas, que a sua dimensão fractal está entre 2 e 3 e, enfim, definir conjuntos de pontos sobre uma linha cuja dimensão fractal está entre 0 e 1.

(...) A geometria fractal é caracterizada por duas escolhas: a escolha de problemas no seio do caos da natureza, uma vez que descrever todo caos seria uma ambição sem esperança e sem interesse, e a escolha de ferramentas no seio das matemáticas, pois procurar aplicações das matemáticas pelo simples fato de serem belas acabou sempre por causar dissabores.

Depois de progressivamente amadurecidas, estas duas escolhas criaram algo de novo: entre o domínio do caos desregulado e a ordem excessiva de Euclides existe agora a nova zona da ordem fractal."

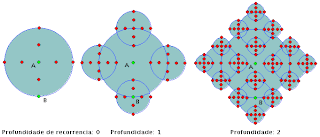
A geometria fractal foi criada, em 1975, pelo matemático francês nascido na Polônia, Benoit Mandelbrot. Em linhas gerais, um fractal é um objeto geométrico que pode ser divido em partes, cada uma da qual semelhante ao original. Essas figuras de forma irregular e fragmentada são encontradas na natureza ou podem ser produzidas artificialmente através de um algoritmo matemático.

Referência: MANDELBROT, B. 1998. Objetos Fractais (Introdução). Lisboa: Editora Gradiva.